* 본 자료는 출간된 자료나 출간 예정 자료의 내용을 요약해서 읽기 쉽게 정리한 것입니다.
연재자료실의 연재글과 통계 데이터는 타 게시물로 옮겨가시는 것을 불허합니다.
14_대표값이란 무엇일까?
이번 장에서는 우리가 흔히 말하는 '평균'이라는 개념을 한번 알아볼께요.
통계학에서는 데이터를 효율적으로 통계내기 위해 가장 대표적인 값들을 산정합니다.
그 중에서 가장 많이 쓰는 대표값이 '평균'인데요....
사실 평균 말고도 대표할 수 있는 값은 많답니다.
예를 들어봅시다.
강남 어느 지역의 집 값이 11억, 13억, 15억, 17억, 20억 등 인데,
한 집만 150억짜리 집이 있는 거에요....
이것을 평균으로 계산하면, 강남의 집 값은 40억 쯤 되겠네요.
그런데, 150억 짜리 집 값이 너무 높아서 평균이 40억이 된거지,
실은 150억짜리 집을 빼면 평균은 15억 수준이랍니다.
이럴 때는 평균 보다는 강남에 있는 모든 집 값을 오름차순이나 내림차순 등으로 나열한 뒤
가장 중앙에 있는 값을 대표 집값으로 정하는 게 평균보다 훨씬 대표적인 값이 되겠죠?
이럴 때는 평균이 아닌 중앙값이 대표값이 된답니다.
반면, 어떤 패션쇼에서 A, B, C 디자이너의 옷들이 있는데,
옷을 구매하는 젋은 여성 상당수가 A, B 디자이너의 다양한 옷들을 선호했어요.
하지만 실제 C 디자이너의 옷 중 D라는 제품 하나의 인기가 폭발적이여서
단일 옷으로는 D라는 제품의 선택률은 가장 높았답니다.
그럼 1등한 옷은 A, B 디자이너의 제품이 아니라 C 디자이너가 만든 D 제품이겠죠?
이럴 때는 평균값이나 중앙값이 아니라 가장 많이 선택된 값, 즉 최빈값이 대표값이 된답니다.
즉, 대표값이란 데이터를 가장 효율적으로 분석하고 시각적으로 활용하기 위한 값으로
평균값, 중앙값, 최빈값 등 데이터를 설명할 수 있는 값 중 가장 가독성이 높은 값을 선택하는 거죠.

15_평균값과 중앙값을 표현해볼까요?
대표값은 어떤 값을 평균으로 산정하느냐이기 때문에 대표값 자체를 AVERAGE라고 말해요.
단, 엑셀에서는 산술적인 평균값을 가장 많이 사용하므로 우리가 흔히 말하는
전체 숫자의 합 / 전체 숫자의 수 = AVERAGE라고 표현해서
더하기는 SUM, 곱의 평균은 AVERAGE로 그냥 표현하죠.
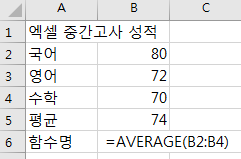
위에서 처럼, 흔히 우리가 쓰는 엑셀함수에서 평균은 average 입니다.
하지만 실제 평균값은 전체 수치를 합한 뒤 평등하게 각 값으로 나눈 값이므로
Average가 아니라 Mean(평등값)이라고 표현합니다.
spss 등 다양한 통계 프로그램에서 평균값을 계산하는 함수는 mean이니까 꼭 알아두세요.
반면, 중앙값은 Median이라고 합니다.
중앙값은 데이터를 크기 순서로 나열했을 때, 가장 가운데 값을 말해요.
만약 가운데 값이 2개라면 그 두 개의 값을 더한 뒤 2로 나눈 값이죠.
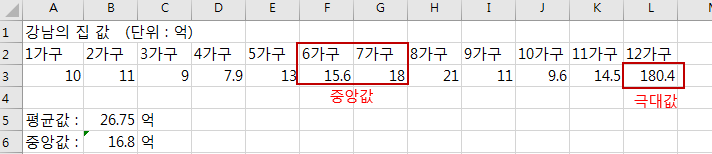
위 엑셀 표에서 보면 강남의 집값은 보통 10~20억 사이인데, 실제 평균은 26.75억이나 됩니다.
그 이유는 12번 가구의 집값이 비정상적인 극대값으로 180억이나 되기 때문이죠.
이럴 때는 평균값보다 중앙값인 16.7억이 훨씬 더 유의미한 대표값이 된답니다.
중앙값은 가장 중앙에 있는 값이므로,
데이터의 중앙값을 기준으로 중앙값보다 작은 값과 큰 값의 숫자는 딱 50%씩으로 같겠죠?
그래서 중앙값을 대표값으로 산정하면, 좌우의 값이 같은 그래프를 만들기 편하답니다.
여기서 하나 더... !!!
만약 극대값을 모두 제거하거나, 극대랎을 평균값에 대응하는 값으로 변환한다면
중앙값보다 평균값을 사용하는게 더 정확할 수도 있겠죠?
통계학에서는 실제 값을 구하기 위해 극대값이 무엇인지를 산정해서 평균을 구하기도 해요.
그래서 나중에 극대값을 제거하고 평균을 구하는 공식도 공부해볼꺼에요.
(알아두면 직장에서 상사님들에게 칭찬받는 꿀팁이랍니다.)
그럼 왜 중앙값을 Median이라고 할까요?
이건 미디어(Media)말과 관련있답니다.
언론기관에서 정보를 전달하는 매체를 미디어(Mass Media)라고 하는데,
미디어는 중간이라는 단어인 Medium의 복수형이죠.
보통 언론인들이 정보를 전달할 때는 좌파니 우파니, 보수니 진보니 하는 입장을 버리고
최대한 중립을 지켜서 가운데 입장에서 내용을 전달해야 합니다.
즉 정보와 사람 사이에서 중간값, 또는 산에 오를 때 가장 높은 산봉우리에서 객관적으로 내려다 보는 값....
이런 걸 미디어라고 하기 때문에 통계학에서 중앙값의 함수는 Median 이라고 해요.
16_최빈값이란 무슨 의미일까요?
반면, 최빈값은 함수로 mode입니다.
혹시 의류회사 중에 인디언 모드라는 말이나
게임 중 자주 내가 사용하는 방식을 무슨 '모드 전환' 이라고 사용한 적 있나요?
또는 사회적인 어떤 흐름이 바뀌었을 때, 특정 '메타'가 등장했다거나 어떤 '모드'로 돌입했다는 말도 씁니다.
즉, 모드는 어떤 사회적, 상황적, 개인적인 유행, 출현빈도 등을 뜻하는 말이에요.
쉽게 말해 어떤 옷을 내가 입을 때, 가장 출현횟수가 많은 옷차림을 분석해서
A 모드를 선호한다거나 B 모드로 전환했다는 말을 사용하는 거죠.
즉, 최빈값은 데이터에서 가장 많이 출현하는 값을 대표값으로 산정하여
유행, 출현빈도, 기호, 판매량 등을 계산할 때 쓰는 대표값이랍니다.
최빈값은 가장 많이 출현한 빈도를 중앙값으로 하기 때문에
통계값을 구할 때 가장 극단값의 영향을 적게 받는다는 장점이 있죠.
반면, 최빈값은 기준이 되는 값의 구간을 정하지 않으면 잘못된 값을 산정한다는 단점이 있습니다.
아래 엑셀표를 한 번 보세요. 70~80KG까지 몸무게를 통계낸 결과 최빈값은 78KG입니다.

그런데 실제 몸무게 분포는 70~74KG 사이에 집중되어 있어요.
즉 72~73 구간에 가장 분포가 많은데, 78을 최빈값으로 잡게 된 거죠.
그래서 최빈값을 구할 때는 기준이 되는 구간을 잡고 시작한답니다.
몸무게의 최빈값을 구하는 구간을 70~74구간 / 75~79구간으로 나누면
당연히 70~74구간이 훨씬 많아지죠?
이렇게 구간을 나눠서 최빈값을 정하면 통계를 쉽게 파악할 수 있습니다.
이 때 구간을 나누는 데이터를 도수라고 하고, 구간의 값을 계급이라고 부르기 때문에
이렇게 최빈값의 구간을 나눠서 만든 그래프를 도수분포표라고 해요.
도수분포표를 만드는 엑셀 정렬함수는 나중에 자세히 설명해드릴께요.
자, 그럼 여기까지 이해했으면 다음 장 부터는
산술평균값을 구하는 공식 중에 기하평균과 조화평균의 원리와 엑셀함수를 알아보고,
최빈값을 가지고 도수분포를 만드는 법과
극대값을 제거해서 업무 보고서를 만드는 방법을 같이 이야기해볼께요.
그리고 다음 장부터는 읽고 따라하셔야 하니,
저의 내용 설명과 첨부된 이미지 아래에 실제 엑셀 또는 SPSS 파일이 첨부되어 있을 거에요.
저희가 기초학습능력 진단 보고서나 직업기초능력 진단 보고서, 산학수요 보고서, 통계리서치 보고서를 쓸 때도
평균값을 산출해서 데이터를 나열하는 방법은 상당히 많이 사용한답니다.
단, 순서값(RANK)이나 교정값은 일반 보고서나 논문에서는 잘 사용하지 않아서 여기서는 생략했지만
이야기하다가 필요하면 설명해드릴께요.
그럼 본격적인 엑셀 함수에 도전해볼까요?
(본 과정에서는 엑셀을 기준으로 함수 사용법을 이야기할 것입니다.
SPSS 사용 전략은 엑셀 함수가 모두 이해된 뒤에 진행할꺼에요.)
'연재자료실' 카테고리의 다른 글
| 대학생 온라인 기초학습능력진단 프로그램 진행 과정 (0) | 2020.05.07 |
|---|---|
| 읽고 따라하는 통계학(11장~13장) (0) | 2020.05.01 |
| 읽고 따라하는 통계학 (9~10장) (0) | 2020.05.01 |
| 읽고 따라하면서 끝내는 통계학(6~8) : 추론 통계학의 이해 (0) | 2020.02.18 |
| 2019년도 대학기초학습능력평가 전체 대학 분석률 총합 (0) | 2020.02.06 |


